Determining the "squelch" status of a received signal:
One of the most obvious ways to determine the presence of a signal is to compare the signal strength against a pre-set threshold: If the signal is above that threshold it is considered to be "present" and an audio gate is opened so that it may be heard.
This sounds like a good way to do it - except that it isn't, really, at least not with FM signals.
If you were listening to an FM signal on 10 meters that was fading in and out (as it often does!) one would have to set the threshold just above that of the background noise - or "open" (e.g. disable) it completely to prevent it from disappearing when the signal strength dove into a minimum during QSB. If the background noise were to vary - as it can over the course of a day and with propagation - the squelch would be prone to opening and closing as well.
As it turns out, typical FM squelch circuits do not operate on signal strength as there are better methods for determining the quality of the signal being received that can take advantage of the various properties of the FM signals themselves.
Making "Triangle Noise" useful:
Mentioned in the previous entry on this topic was "Triangle Noise", so-called by the way it is often represented graphically.
High-pass filtering to detect (only) "squelch noise":
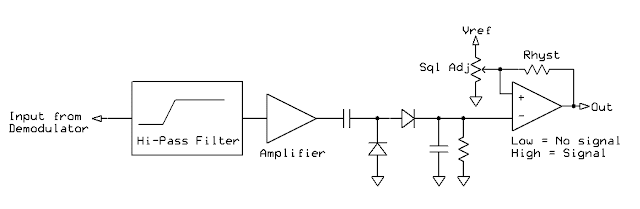
From the above drawing in Figure 1 it can be recognized that if we only "listen" to the high-frequency audio energy that passes through the "Squelch noise" high-pass filter all we are going to detect is the noise level, independent of the modulated audio. If we base our signal quality on the amount of noise that we detect at these high frequencies - which are typically above the typical hearing range (usually ultrasonic, above 10 kHz) - we can see that we don't need to know anything about the signal strength at all.
This method works owing to an important property of FM demodulators: The amount of recovered audio does not change with the signal strength as the demodulator is "interested" only in the amount of frequency change, regardless of the actual amplitude. What does change is the amount of noise in our signal as thermal noise starts to creep in, causing uncertainty in the demodulation. In other words, we can gauge the quality of the signal by looking only at the amount of ultrasonic noise coming from our demodulator.
An analog representation of a squelch circuit may be seen in Figure 2. For the simplest circuit, the high-pass filter could be as simple as an R/C differentiator followed by a single-transistor amplifier, and the same sorts of analogs (pun intended!) could be applied in software.
After getting the mcHF FM demodulator to be functional I tried several different high-pass filter methods - including a very simple differentiator algorithm such as that described in the previous posting - except, of course, that the "knee" frequency was shifted far upwards. The absolute value was then taken from the output of the high-pass filtered and smoothed and printed on the screen while the input signal, modulated with a 1 kHz audio sine wave and fed to a SINAD meter (read about SINAD here - link) while signal level was varied: In this way I could see how the output of the noise detection circuit behaved with differing signal conditions.
In doing this testing I noted that a simple differentiator did not work as well as I'd hoped - likely due to the fact that unlike an analog circuit in which the high-frequency energy can continue to increase in intensity with frequencies well into the 10's or 100's of kHz, in the digital domain we have a "hard" limit enforced by Nyquist, stopping at 23 kHz or so on the mcHF with its 48 ksps rate.
With less high frequency spectral noise energy (overall) to work with it is necessary to amplify the output of a simple differentiator more, but this also brings up the lower frequency (audio) components, causing it to be more affected by speech and other content, requiring a better filter. Ultimately I determined that 6-pole IIR high-pass audio filter with a 15 kHz cut-off frequency, capable of reducing "speech" energy and its second and third harmonics below 9-10 kHz by 40-60dB, worked pretty well: In testing I also tried a similar filter with an 8 kHz cut-off, but it was more-affected by voice modulation and its immediate harmonics.
Comment:
If the FM demodulation is working properly the result will be a low-distortion, faithful representation of the original audio source with little/no energy above the low-pass filter's cut-off in the transmitter. If the signal is distorted in some way - such as with multipath distortion, being off-frequency or with excess deviation, energy from this distortion can appear in the ultrasonic region which cannot be easily distinguished from "squelch" noise.
If this energy is high enough, the squelch can close inadvertently since the signal may be "mistaken" as being weak: This is referred to as "squelch clamping" and is so-called as it is often seen on voice peaks of signals degraded by multipath and/or off-frequency.
Determining noise energy:
In short, the algorithm to determine the squelch energy was as follows:
loop:
squelch_avg = (1-α) * squelch_avg + sqrt(abs(hpf_audio)) * α
if(squelch_avg > MAX_VALUE)
squelch_avg = MAX_VALUE
Where:
α = "smoothing" factor
hpf_audio = audio samples that have been previously high-pass filtered to remove speech energy
squelch_avg = the "smoothed" squelch output
If you look at the above pseudocode example you'll notice several things:
- The square root value of the absolute value of the high-pass noise energy is taken. It was observed that as the signal got noisier, the noise amplitude climbed very quickly: If we didn't "de-linearize" the squelch reading based on the noise energy - which already has a decidedly non-linear relationship to the signal level - we would find that the majority of our linear squelch adjustment was "smashed" toward one end of the range. By taking the square root our value increases "less quickly" with noisier signals than it otherwise would.
- The value "squelch_avg" is integrated (low-pass filtered) to "smooth" it out - not surprising since it is a measurement of noise which, by its nature, is going to vary wildly - particularly since the instantaneous signal level can be anything from zero to peak values. What we need is a (comparatively) long-term average.
- The "squelch_avg" value is capped at "MAX_VALUE". If we did not do this the value of "squelch_avg" would get very high during periods of no signal (maximum noise) and take quite a while to come back down when a signal did appear, causing a rather sluggish response. The magnitude of "MAX_VALUE" was determined empirically by observing "squelch_avg" with a rather noisy signal - the worst that would be reasonably expected to open a squelch.
The above "squelch_avg" value increases as the quieting of the received FM signal decreases which means that we must either invert this value or, if a higher "squelch" setting means that a better signal is required for opening the squelch, that same "squelch setting" variable must have its sense inverted as well.
I chose the former approach, with a few additional adjustments:
- The "squelch_avg" value was rescaled from its original range to approximately 24 representing no-signal conditions to 3 representing a full-quieting signal with modulation with hard limits imposed on this range (e.g. it is not allowed to exceed 24 or drop below 3).
- The above number was then "inverted" by subtracting it from 24, setting its range to 2 representing no signal to 22 for one that is full-quieting with modulation.
The final step was to make sure that if the squelch was set to zero that it was unconditionally open - this, to guarantee so that no matter what, some sort of signal could be heard without worrying about the noise threshold occasionally causing the squelch to close under certain conditions that might cause excess ultrasonic energy to be present.
The result is a squelch that seems to be reasonably fast in response to signals, weak or strong, but very slightly slower in response to weak signals. This slight asymmetry is actually advantageous as it somewhat reduces the rate-of-change that might occur under weak-signal conditions (e.g. squelch-flapping) - particularly during "mobile flutter." The only downside that is currently noted is that despite the "de-linearization" the squelch setting is still somewhat compressed with the highest settings being devoted to fairly "quiet" signals" and most of the range representing somewhat noisier signals - but in terms of intelligibility and usability, it "feels" pretty good.
Subaudible tone decoding:
One useful feature in an FM communications receiver is that of a subaudible tone (a.k.a. CTCSS) decoder. For an article about this method of tone signalling, refer to the Wikipedia article here - link.
In short, this method of signalling uses a low-frequency tone, typically between 67 and 250 Hz, to indicate the presence of a signal and unless the receiver detects this tone on the received signal it is ignored. In the commercial radio service this was typically used to allow several different users to share the same frequency but to avoid (always) having to listen to the others' conversations. In amateur radio service it is often used as an interference mitigation technique: The use of carrier squelch and subaudible tone greatly reduces the probability that the receiver's squelch will falsely open if no signal is present or, possibly, if the wrong signal - in the case where a listener is an an area of overlapping repeaters - is present - but this works only if there is a tone being modulated on the desired signal in the first place.
The Goertzel algorithm:
There are many ways to detect tones, but the method that I chose for the mcHF was the Goertzel algorithm. Rather than explain exactly how this algorithm works I'll point the reader to the Wikipedia article on the subject here - link. The use of the Goertzel algorithm has several distinct advantages:
- Its math-intensive parameters may be calculated before-hand rather than on the fly.
- It requires only simple addition/subtraction and one multiplication per iteration so it need only take a small amount of processor overhead.
- Its detection bandwidth is very scalable: The more samples that are accumulated, the narrower it is - but also slower to respond.
The Goertzel algorithm, like an FFT, will output a number that indicates the magnitude of the signal present at/about the detection frequency, but by itself this number is useless unless one has a basis of comparison. One approach sometimes taken is to look at the total amount of audio energy, but this is only valid if it can be reasonably assured that no other content will be present such as voice or noise, which may be generally true when detecting DTMF, but this cannot be assured when detecting a subaudible tone in normal communications!
"Differential" Goertzel detection:
I chose to use a "differential" approach in which I set up three separate Goertzel detection algorithms: One operating at the desired frequency, another operating at 5% below the desired frequency and the third operating at 4% above the desired frequency and processed the results as follows:
- Sum the amplitude results of the -5% Goertzel and +4% Goertzel detections.
- Divide the results of the sum, above, by two.
- Divide the amplitude results of the on-frequency Goertzel by the above sum.
- The result is a ratio, independent of amplitude, that indicates the amount of on-frequency energy. In general, a ratio higher than "1" would indicate that "on-frequency" energy was present.
- We obtain a "reference" amplitude that indicates how much energy there is that is not on the frequency of the desired tone as a basis of comparison.
- By measuring the amplitude of adjacent frequencies the frequency discrimination capability of the decoder is enhanced without requiring narrower detection bandwidth and the necessarily "slower" detection response that this would imply.
Setting the Goertzel bandwidth:
One of the parameters not easily determined in reading about the Goertzel algorithm is that of the detection bandwidth. This parameter is a bit tricky to discern without using a lot of math, but here is a "thought experiment" to understand the situation when it comes to being able to detect single-frequency (tone) energy using any method.
Considering that the sample rate for the FM decoder is 48 ksps and that the lowest subaudible tone frequency that we wish to detect is 67.0 Hz, we can see that at this sample rate it would take at least 717 samples to fully represent just one cycle at 67.0 Hz. Logic dictates that we can't just use a single cycle of 67 Hz to reliably detect the presence of such a tone so we might need, say, 20 cycles of the 67 Hz tone just to "be sure" that it was really there and not just some noise at a nearby frequency that was "near" 67 Hz. Judging by the very round numbers, above, we can see that if we had some sort of filter we might need around 15000 samples (at 48 ksps) in order to be able to filter this 67 Hz signal with semi-reasonable fidelity.
As it turns out, the Goertzel algorithm is somewhat similar. Using the pre-calculated values for the detection frequency, one simply does a multiply and a few adds and subtractions of each of the incoming samples: Too few samples (fewer than 717 in our example, above) and one does not have enough information with which to work at low frequencies to determine anything at all about our target frequency of 67 Hz, but with a few more samples one can start to detect on-frequency energy with greater resolution. If you let the algorithm run for too many samples it will not only take much longer to obtain a reading, but the effective "detection bandwidth" becomes increasingly narrow. The trick is, therefore, to let the Goertzel algorithm operate for just enough samples to get the desired resolution, but not so many that it will take too long to obtain a result! In experimentation I determined that approximately 12500 samples were required to provide a tradeoff between adequately-narrow frequency resolution and reasonable response time.
This is part of the reason for the "differential" Goertzel energy detection in which we detect energy at, above and below the desired frequency: This allows us to use a somewhat "sloppier" - but faster - tone detection algorithm while, at the same time, getting good frequency resolution and, most importantly, the needed amplitude reference to be able to get a useful ratiometric value that is independent of amplitude.
Debouncing the output:
While an output of greater than unity from our differential Goertzel detection generally indicates on-frequency energy, one must use a significantly higher value than that to reduce the probability of false detection. At this point one can sort of treat the output of the tone detector as a sort of noisy pushbutton switch an apply a simple debouncing algorithm:
loop:
if(goertzel_ratio >= threshold) {
debounce++
if(debounce > debounce_maximum)
debounce = debounce_maximum
}
else {
if(debounce > 0)
debounce--
}
if(debounce >= detect_threshold)
tone_detect = 1
else
tone_detect = 0
where:
"goertzel_ratio" is the value "f/((a+b)/2))" described above where:
f = the on-frequency Goertzel detection amplitude value
a = the above-frequency Goertzel detection amplitude value
b = the below-frequency Goertzel detection amplitude value
"threshold" is the ratio value above which it is considered that tone detection is likely. I found 1.75 to be a nice, "safe" number that reliably indicated on-frequency energy, even in the presence of significant noise.
"detect_threshold" = the number of "debounce" hits that it will take to consider a tone to be valid. I found 2 to be a reasonable number.
"debounce_maximum" is the highest value that the debounce count should attain: Too high and the it will take a long time to detect the loss of tone! I used 5 for this which causes a slight amount of effective hysteresis and a faster "attack" than "decay" (e.g. loss of tone).
With the above algorithm - called approximately once every 12500 samples (e.g. just under 4 times per second with a 48ksps sample rate) - the detection is adequately fast and quite reliable, even with noisy signals.
Putting it all together:
 |
| Figure 3: An FM signal with a subaudible tone being detected, indicated by the "FM" indicator in red. |
Finally, if the squelch is closed (audio is muted) the audio from the FM demodulator is "zeroed".
* * *
In a future posting I'll describe how the the modulation part of this feature was accomplished on the mcHF along with the pre-emphasis of audio, filtering and the generation of burst and subaudible tones.
[End]
This page stolen from "ka7oei.blogspot.com".